Estimating the number of possible chess games

Counting the games of chess — analyzing our chess databases, running some simulations, and making hydrogen bombs.

It’s commonly known that the total number of possible chess games exceeds the total number of atoms in the observable universe, which at first seems surprising given only 64 squares and a fairly small set of rules for the pieces, but, as you’ll find out, it gets even better.

Another simple and well known example of how easily small permutations become astronomical is the number of ways a deck of standard playing cards can be arranged. The number is so huge that whenever you shuffle a deck of cards you are the only person to have ever had that arrangement of cards in your hands. In fact, what I just said doesn’t come anywhere close to doing justice to that number.

Anyways, the number of chess games is on a level far beyond that, and estimating it is much more interesting of a problem.

Programming a Computer for Playing Chess

In 1949, Claude Shannon wrote a paper on programming a computer for playing chess. Back in the day, computers doing complex logical tasks was a new thing, and it had started this whole new philosophical debate on whether those machines could actually be considered intelligent the way humans are, or what it meant for anything to be intelligent for that matter. One of the ways computer scientists came up with to test it was if those computers could be programmed to play chess, potentially against a grandmaster or so. But anyways, no one cares, and chess AI would make a post too long for this newsletter.

In that paper, Shannon gave his estimate of the number of possible chess games to be around 10¹²⁰ (the number of atoms in the observable universe is ~10⁸⁰).

How he came up with the number was by assuming the average legal moves in any given position to be 30, and the average length of a chess game to be 80 plies (a ply is when one piece is moved by either one of the sides, when both the sides do a ply, that’s called a move). I found this cool live statistic for the average length of a chess game and this cool stack exchange answer on average number of legal moves. The current more precise values are 40.67 moves (81.3 plies) per game and 31.1 legal moves in any given position on average; Shannon made good assumptions, and 7 decades of added chess theory has barely shifted the average.

So, an average game of chess looks like this: white picks from one of it’s 30 legal moves, after which black picks one of it’s 30, and it continues until 80 plies are reached. The total positions that can be reached this way are 30 × 30 × 30 × 30 … 80 times, i.e, 30⁸⁰, which roughly estimates to 10¹²⁰. Here’s how to do quick conversions like that, in case you’re wondering:

30⁸⁰ = (10 × 3)⁸⁰
= 10⁸⁰ × 3⁸⁰
= 10⁸⁰ × (10^log3)⁸⁰
= 10⁸⁰ × 10^{(log3 × 80)}
= 10⁸⁰ × 10^{(0.477 × 80)} [log3 = 0.477]
= 10⁸⁰ × 10^38.16
= 10^{(80 + 38.16)}
≈ 10¹²⁰

It seems like a reasonable estimate. However, there’re a few problems. Before we can talk about them, let’s talk a couple of other things.

Longest possible chess game

Calculating the longest possible length of a chess game is a bit complex. You can skip next three paragraphs if you don’t care much about the explanation.

Given the 75 move rule, the longest chess game possible would look something like having repetitive 74.5 back and forth moves, followed by a capture or a pawn move, and another 74.5 back and forth moves, where we try to keep as many pieces on the board as possible.

After every 74.5 moves, one capture or pawn move resets the counter, and we can have another 74.5 repetitive moves. That is, if black does all reset moves. There’s some sweet spot between dividing those reset moves between black and white to maximize the game length. Turns out you need to switch who plays the next reset move only three times; starting from black to white, then again to black, and finally to white. Though, every time you perform the switch, it has to be done on the 74th move, because by 74.5, you wouldn’t have a ply left and it would be a draw.

From the starting position, pushing the pawns further until you can’t, assuming no resistance from other side, would give you 8*6*2 = 96 total pawn moves. However, in order to cross each other, all pawns from one side will have to capture one piece each from the other side, placed precisely to allow crossing. Total possible captures in a chess game are 30, out of which 8 would have to from pawns to allow crossing. Therefore, we end up with 96 + 30 - 8 = 118 number of possible moves that can be used to reset the 75 move counter, and the reset control switching 3 times.

Giving us 118 * 75 - 3 * 0.5 = 8848.5 moves (17697 plies) to be the maximum possible length of a chess game.

Guess who did all the work of simulating the full longest possible chess game out there and exporting it just for a substack post? Haha, not me, I stole it from this guy. You can check it out here.

The longest game ever played in a chess tournament lasted 269 moves. Just by looking at the difference in those two numbers, we can tell that the number of possible games lasting more than 269 moves would be far greater than the number of games lasting less than 269 moves.

Let’s assume the chess database we referred to earlier had all possible chess games under 269 moves, so that adding any game longer than 269 moves would have the least possible impact on the average game length. Though, the average would still be shifted to a slightly higher value. How much higher would it go from 40 moves (80 plies) if we fed all possible games bigger than 269 moves into the database? One more number before we get to that.

Maximum legal moves in a position

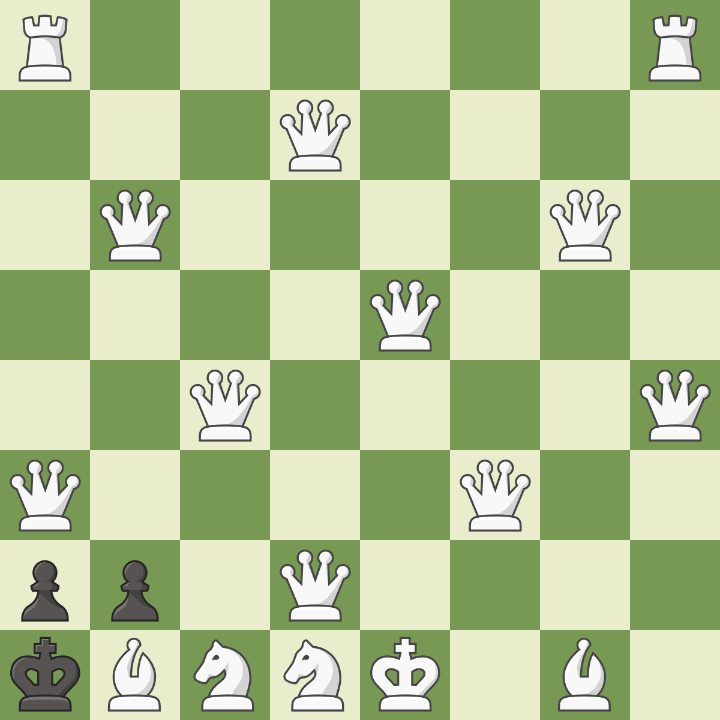
The highest possible number of legal moves in a position are 218, in this position:

A position with 9 queens is rare. However, given it’s practical non-existence in our databases, and the number of legal moves available here deviating far from our current average of 30, the impact of positions like these taken into account would be very significant on our average.

Since our current databases represent positions with lower legal moves in proportions more closer to the proportion of actual number of such positions out of the total, we can tell that accounting for such positions outside of our databases would shift the average to some higher value as well. Shannon’s assumptions weren’t so good after all.

Note: While Shannon’s number has practically no insight, the approach Shannon took can still be used to estimate the number of *sensible* chess games, games where you’re not doing obvious dumb stuff. Instead of an average of 30 legal moves, we assume an average of around 3 sensible moves per ply. That gives the number total sensible chess games to be around 3^80 (~10^40).

Bounds

Now that we know that the average legal moves in a position are at least 30, and the average length of a game is at least 80. Shannon’s number, 10¹²⁰, can probably serve as a good lower bound for what the actual number of chess games might be.

For the upper bound, we could map the longest possible game with the highest possible legal moves per position, giving us 218¹⁷⁶⁹⁷ (~ 10⁴¹²³⁴).

Yay, we’ve made progress. After all of what we’ve done, we’ve been able to narrow down our answer to be somewhere within the range of 10¹²⁰ to 10⁴¹²³⁴.

Anyways, we need to do better. It’s hard to find what the number of possible chess games is. In the rest of this post, we’ll try to narrow our bounds further until we’ve come up with something more acceptable.

From our starting point of Shannon’s number, we discovered and resolved a few logical inconsistencies in our approach. Enough inconsistencies that you should probably start to doubt for there to be something fundamentally wrong with our process so far. Somewhere above we made one blunder that led all of the logical inconsistencies that followed.

Monte Carlo Simulations

During world war 2, inside the Manhattan Project meant for nuclear weapons research, this guy called Stanislaw Ulam was wasting his working hours playing solitaire. Though, being a mathematician, he wondered what the probability of him winning a random solitaire game was. After failing to figure out all the combinatorics himself, he decided to also waste the working hours of this other guy, John Von Neumann. Ulam asked Neumann to simulate solitaire games for him on this fancy new ENIAC thing that was out recently.

The plan was to simulate, let’s say, N random solitaire games, and have the computer play them through to figure out how many of them were winnable, let’s say, n. Then the probably of a random game of solitaire being winnable would’ve simply been n/N.

They named this method of finding that probability, or more complex probability distributions along similar lines, the Monte Carlo method, after some place in Monaco famous for gambling. The idea was to be able to infer properties about a system that’s far too complex to do standard combinatorics with, by analysing a smaller subset of the possible configurations of the system. Wanna know what the probability distribution of the outcomes of flipping a biased deformed coin will look like? Just flip the coin 10000 times and assume that the delta of going from 10000 to infinity would be negligible.

What we did earlier to find the average legal moves or the average length of a chess game, analyzing millions of recorded chess games, was in fact Monte Carlo… except with a catch.

Side note: The method actually even ended up being useful in the Manhattan Project; it was used to simulate neutron transport stuff (the process by which neutrons move and interact within a material) inside the hydrogen bomb, among other things.

Finding the right subset

While using the Monte Carlo method, it’s extremely important to pick the right subset of the total configurations of the system you’re trying to analyze. It’s not very hard though, you just need to pick a random subset, that’s all. But it has to be random.

Let’s say you’re trying to predict election results, you might start with a twitter poll asking everyone who they plan on voting. By doing so, you’ve already cut down the people who’re 1.) not active on twitter, or 2.) not following you. Given your age, the people who follow you or people who might end up finding your poll would have a somewhat predictable age spectra significantly deviating from an even distribution of all ages. Same goes for their profession, or where they live, or your and their opinions about things that made them follow you in the first place. Even if your poll gets a million responses, it’s highly unlikely that you’ll get anything other than just noise out of it.

All of our recorded chess games, or the countless games Stockfish or any chess engine ever played with itself for it’s training, are all like the responses to that poll. They’re not truly random. All they have is just noise. They cannot be used for Monte Carlo, but Shannon did, and we continued from his work.

Btw, funny how our recorded games are all noise because they are not random enough, almost as if the randomness somehow contains the information we need inside it, try looking up something along these lines, you might find some cool stuff.

The only valid games that we can use for our purpose are games where both the sides simply pick one random move out of all the legal moves available at any point in the game.

Now that we know where we went wrong, we can start few things over.

Number of possible chess games = (average legal moves)^{(average length of a game)}

where the dataset we use to find the averages now comes from a computer playing millions of chess games, all with entirely random moves.

Before we ask our computer to do that, there’s another small issue to address, the subset should also be large enough. You cannot flip the deformed coin just 10 times and hope to get an accurate probability distribution. Given we’re talking numbers far beyond astronomical, a simulation running any realistic number of chess games would probably have very high error.

Back to our bounds

Let’s change our rules of chess a tiny bit. Let’s say a game of chess has to be exactly 17697 plies. Now for this version of chess, we’ve narrowed the total possibilities significantly, implying if we ran a simulation of a million games for just this scenario, we’d get much less error in our results. Running a simulation like that gives the average legal moves that also lead to the game lasting 17697 plies to be around 32.8 (branching factor is the term for it, it’s the average children a graph node has; in our case, it’s the ratio by which the number of possible games increases with each added ply, i.e. every added ply on average increases the total possible games that can be played till that ply by 32.8 times on average). I did not run the simulation myself, that too was this guy. All credit to François, none of the numbers here are my own. I don’t think I would’ve gained any significant extra insight out of running the simulations myself.

Using that branching factor, the number of possible games with exactly 17697 plies comes out to be 32.8¹⁷⁶⁹⁷ (~ 10²⁶⁸²⁷ ). Since the set of all chess games with exactly 17697 plies is a subset of the set of all of the chess games, the number we just came up with has to be less than the number of total chess games out there. Therefore, we can move our lower bound for possible chess games to be at least around 10²⁶⁸²⁷.

Now we’ve made some actual progress, the number of possible chess games is somewhere between 10²⁶⁸²⁷ to 10⁴¹²³⁴. We can do a lot of things to make our range narrower. François also has a post where he plotted the branching factors for different lengths of games and, after doing some curve fitting and ignoring the 75 moves rule, found that the series should converge to a maximum of around 84.3, giving 84.3¹⁷⁶⁹⁷ (~ 10³⁴⁰⁸²) to be the upper bound for maximum number possible chess games.

This number is so big that if we had a multiverse where the number of universes was the same as the number of atoms in our universe, and then a multiverse of those multiverses, and then a multiverse of those even bigger multiverses, we’d have to do that 8 times to reach the atoms count close to the number of possible chess games, and even then we could still fit a crazy amount of more universes.

Conclusion

Chess is too complex for combinatorics. By analyzing out databases of games, we can make some statistical statements about the game. Some other statements need databases of games entirely different from what we maintain the databases of. Our final estimates of 10²⁶⁸²⁷ to 10³⁴⁰⁸² can still be somewhat wrong, we made a lot of gallant assumptions on our way there. We can come up with better numbers by not being so easy with our approximations or running longer simulations.

But it doesn’t really matter, the number itself barely has any significance. What’s nice is all the clever number handling we could do in this post to keep things simple enough that you were (hopefully) able to do all the maths entirely in your head, or how we could connect the dots from chess to twitter polls to nuclear research, or how thinking about solitaire over a weekend could probably help you with your hydrogen bomb.